Friday, 6 February 2015

Strassen Algorithm

Concept(Source Wikipedia):
Let A, B be two square matrices over a ring R. We want to calculate the matrix product C as
\mathbf{C} = \mathbf{A} \mathbf{B} \qquad \mathbf{A},\mathbf{B},\mathbf{C} \in R^{2^n \times 2^n}
If the matrices A, B are not of type 2n x 2n we fill the missing rows and columns with zeros.
We partition A, B and C into equally sized block matrices
\mathbf{A} = \begin{bmatrix} \mathbf{A}_{1,1} & \mathbf{A}_{1,2} \\ \mathbf{A}_{2,1} & \mathbf{A}_{2,2} \end{bmatrix} \mbox { , } \mathbf{B} = \begin{bmatrix} \mathbf{B}_{1,1} & \mathbf{B}_{1,2} \\ \mathbf{B}_{2,1} & \mathbf{B}_{2,2} \end{bmatrix} \mbox { , } \mathbf{C} = \begin{bmatrix} \mathbf{C}_{1,1} & \mathbf{C}_{1,2} \\ \mathbf{C}_{2,1} & \mathbf{C}_{2,2} \end{bmatrix}
with
\mathbf{A}_{i,j}, \mathbf{B}_{i,j}, \mathbf{C}_{i,j} \in R^{2^{n-1} \times 2^{n-1}}
then
\mathbf{C}_{1,1} = \mathbf{A}_{1,1} \mathbf{B}_{1,1} + \mathbf{A}_{1,2} \mathbf{B}_{2,1}
\mathbf{C}_{1,2} = \mathbf{A}_{1,1} \mathbf{B}_{1,2} + \mathbf{A}_{1,2} \mathbf{B}_{2,2}
\mathbf{C}_{2,1} = \mathbf{A}_{2,1} \mathbf{B}_{1,1} + \mathbf{A}_{2,2} \mathbf{B}_{2,1}
\mathbf{C}_{2,2} = \mathbf{A}_{2,1} \mathbf{B}_{1,2} + \mathbf{A}_{2,2} \mathbf{B}_{2,2}
With this construction we have not reduced the number of multiplications. We still need 8 multiplications to calculate the Ci,j matrices, the same number of multiplications we need when using standard matrix multiplication.
Now comes the important part. We define new matrices
\mathbf{M}_{1} := (\mathbf{A}_{1,1} + \mathbf{A}_{2,2}) (\mathbf{B}_{1,1} + \mathbf{B}_{2,2})
\mathbf{M}_{2} := (\mathbf{A}_{2,1} + \mathbf{A}_{2,2}) \mathbf{B}_{1,1}
\mathbf{M}_{3} := \mathbf{A}_{1,1} (\mathbf{B}_{1,2} - \mathbf{B}_{2,2})
\mathbf{M}_{4} := \mathbf{A}_{2,2} (\mathbf{B}_{2,1} - \mathbf{B}_{1,1})
\mathbf{M}_{5} := (\mathbf{A}_{1,1} + \mathbf{A}_{1,2}) \mathbf{B}_{2,2}
\mathbf{M}_{6} := (\mathbf{A}_{2,1} - \mathbf{A}_{1,1}) (\mathbf{B}_{1,1} + \mathbf{B}_{1,2})
\mathbf{M}_{7} := (\mathbf{A}_{1,2} - \mathbf{A}_{2,2}) (\mathbf{B}_{2,1} + \mathbf{B}_{2,2})
only using 7 multiplications (one for each Mk) instead of 8. We may now express the Ci,j in terms of Mk, like this:
\mathbf{C}_{1,1} = \mathbf{M}_{1} + \mathbf{M}_{4} - \mathbf{M}_{5} + \mathbf{M}_{7}
\mathbf{C}_{1,2} = \mathbf{M}_{3} + \mathbf{M}_{5}
\mathbf{C}_{2,1} = \mathbf{M}_{2} + \mathbf{M}_{4}
\mathbf{C}_{2,2} = \mathbf{M}_{1} - \mathbf{M}_{2} + \mathbf{M}_{3} + \mathbf{M}_{6}



C Code:
//Please enter n(order of matrix) of form 2^i
int iop=0,jop=0;
static int resc[2][2];
void rec(int n,int comb[])//FOR GETTING OF EVERY 2*2 matrix
{
    int ri;
    comb[0]=0;
for(ri=1;ri<(n/2)+1;ri++)
{
    comb[ri]=(2*ri)-1;
}
}

recadd(int n,int a[][n],int b[][n],int c[][n],int k,int comb[])//For getting matrices of order 2 by 2 which are to be multiplied
{
    if(n!=2)
    {
    int i,j,ridi;
    {
        int al[2][2],bl[2][2];int l=1;
        int ri=comb[0],rj=comb[1];
        int rms=comb[0],lms=comb[1],lml=1;
        while(lml<=k)
        {
        int rmss=comb[0],lmss=comb[1],lmll=1;
        {
            al[0][0]=a[rms][rmss];al[0][1]=a[rms][lmss];al[1][0]=a[lms][rmss];al[1][1]=a[lms][lmss];
        int ris=comb[0],rij=comb[1],lm=1;
        while(lm<=k)
        {
            int l=1;
        int ri=comb[0],rj=comb[1];
                while(l<=k)
                {
                    for(i=0;i<2;i++)
                    {
                        bl[i][0]=b[ri][ris];
                        bl[i][1]=b[ri][rij];
                        ri=rj;
                    }
                    int tyu,yu;
                   mul(al,bl);
                    rmss=++lmss,lmss=comb[++lmll];
                    al[0][0]=a[rms][rmss];al[0][1]=a[rms][lmss];al[1][0]=a[lms][rmss];al[1][1]=a[lms][lmss];
                    ri=++rj;
                    rj=comb[++l];
                }
                int tyu,yu;
                c[iop][jop]=resc[0][0];c[iop][jop+1]=resc[0][1];c[iop+1][jop]=resc[1][0];c[iop+1][jop+1]=resc[1][1];
jop+=2;
if(jop>n-2){iop+=2;jop=0;}
    resc[0][0]=0;resc[0][1]=0;resc[1][0]=0;resc[1][1]=0;
                ris=++rij;
                rij=comb[++lm];
            rmss=comb[0],lmss=comb[1],lmll=1;
             al[0][0]=a[rms][rmss];al[0][1]=a[rms][lmss];al[1][0]=a[lms][rmss];al[1][1]=a[lms][lmss];
            }
        }
    rms=++lms,lms=comb[++lml];
    }
}
    }
    else{
    mul(a,b);
      int tyu,yu;
                for(tyu=0;tyu<2;tyu++)
                {
                    for(yu=0;yu<2;yu++)
                        {printf("%d ",resc[tyu][yu]);resc[tyu][yu]=0;}
                }
    }
}
mul(int al[][2],int bl[][2])//Strassen Matrix Multiplication
{
    int a1,a2,a3,a4,a5,a6,a7;
    a1=(al[0][0]+al[1][1])*(bl[0][0]+bl[1][1]);
    a2=(al[1][0]+al[1][1])*bl[0][0];
    a3=al[0][0]*(bl[0][1]-bl[1][1]);
    a4=al[1][1]*(bl[1][0]-bl[0][0]);
    a5=(al[0][0]+al[0][1])*bl[1][1];
    a6=(al[1][0]-al[0][0])*(bl[0][0]+bl[0][1]);
    a7=(al[0][1]-al[1][1])*(bl[1][0]+bl[1][1]);
resc[0][0]+=(a1+a4+a7-a5);
resc[0][1]+=(a3+a5);
resc[1][0]+=(a2+a4);
resc[1][1]+=(a1+a3+a6-a2);
}
main()
{
printf("Enter the size of Matrix\n");
int n;
scanf("%d",&n);
int a[n][n];
int b[n][n];
int c[n][n];
int mit,nit;
printf("Enter elements of a\n");
for(mit=0;mit<n;mit++)
{
    for(nit=0;nit<n;nit++)
    {
        scanf("%d",&a[mit][nit]);
    }
}
printf("Enter elements of b\n");
for(mit=0;mit<n;mit++)
{
    for(nit=0;nit<n;nit++)
    {
        scanf("%d",&b[mit][nit]);
    }
}
int k=(n/2)+1;
int comb[k];
k--;
rec(n,comb);
recadd(n,a,b,c,k,comb);
for(mit=0;mit<n;mit++)
{
    for(nit=0;nit<n;nit++)
    {
        printf("%d ",c[mit][nit]);
    }
    printf("\n");
}
}

Time Complexity:

The standard matrix multiplication takes approximately 2N3 (where N = 2n) arithmetic operations (additions and multiplications); the asymptotic complexity is Θ(N3).
The number of additions and multiplications required in the Strassen algorithm can be calculated as follows: let f(n) be the number of operations for a 2n × 2n matrix. Then by recursive application of the Strassen algorithm, we see that f(n) = 7f(n−1) + l4n, for some constant l that depends on the number of additions performed at each application of the algorithm. Hence f(n) = (7 + o(1))n, i.e., the asymptotic complexity for multiplying matrices of size N = 2n using the Strassen algorithm is
O([7+o(1)]^n) = O(N^{\log_{2}7+o(1)}) \approx O(N^{2.8074}).
The reduction in the number of arithmetic operations however comes at the price of a somewhat reduced numerical stability,[3] and the algorithm also requires significantly more memory compared to the naive algorithm. Both initial matrices must have their dimensions expanded to the next power of 2, which results in storing up to four times as many elements, and the seven auxiliary matrices each contain a quarter of the elements in the expanded ones.


Posted by at

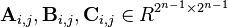
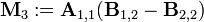
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)